📈 Macro Regime Duration Model
Quantitative Framework for Detecting and Exploiting Macroeconomic State Transitions
🧠 Abstract
A quantitative model that identifies hidden macroeconomic regimes and links them to yield-curve dynamics and dynamic portfolio allocation. Combining Markov-switching econometrics, stochastic processes, and mean–variance optimization, the framework enhances Sharpe ratio and reduces drawdown through regime-conditioned rebalancing.
⚡ TL;DR Highlights
- Built a 3-state Markov-switching model (Recession / Moderate Growth / Expansion) on macro variables.
- Linked macro regimes to Nelson–Siegel yield-curve factors via VAR forecasting.
- Designed a regime-aware portfolio optimizer, achieving: Sharpe +48%, drawdown −45%, volatility −28% vs. static 60/40 benchmark.
- Fully automated pipeline: data → inference → forecast → backtest.
🔍 Overview
The model identifies latent economic regimes from macro indicators (GDP growth, inflation, unemployment) using a 3-state Markov-switching regression. Each inferred regime captures a distinct business-cycle phase characterized by persistence, volatility, and transition probabilities.
Framework components:
- Detects hidden business-cycle regimes
- Estimates regime durations and transition dynamics
- Links regimes to yield-curve behavior
- Applies regime-conditioned portfolio allocation
🧩 Concepts Used
| Domain | Concept | Application |
|---|---|---|
| Time Series Modeling | Markov-Switching Regression | Captures non-linear, regime-dependent GDP dynamics |
| Stochastic Processes | Hidden Markov Models | Infers unobservable macroeconomic states |
| Econometrics | Transition Matrix Analysis | Quantifies persistence and switching probabilities |
| Yield Curve Analysis | Nelson–Siegel Factor Model | Decomposes Treasury yields into Level, Slope, Curvature |
| Forecasting | Vector Autoregression (VAR) | Models regime–yield interactions |
| Portfolio Theory | Mean–Variance Optimization | Allocates assets dynamically by macro-state probability |
⚙️ Model Pipeline
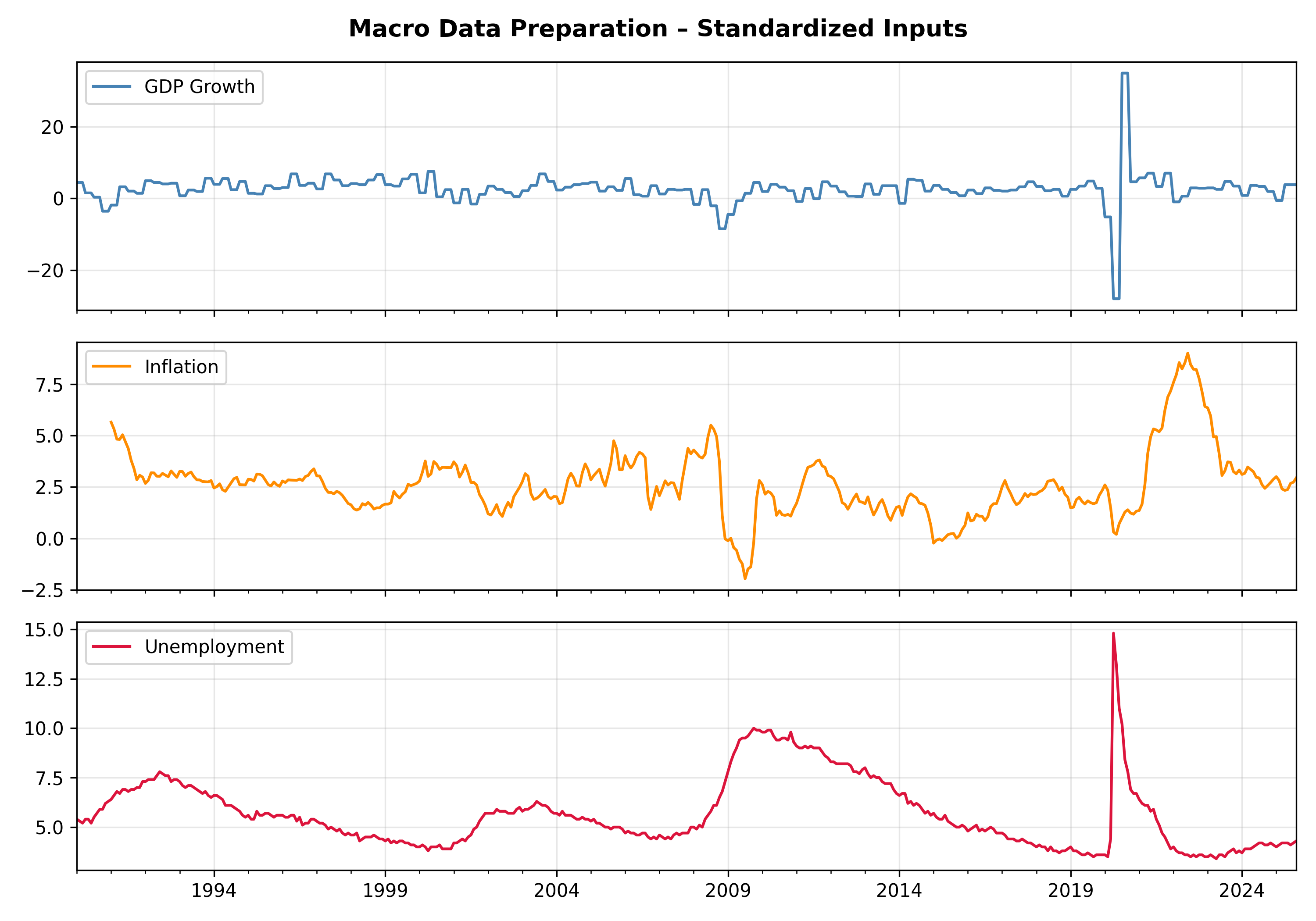
1️⃣ Data Preparation
Standardized GDP, inflation, and unemployment data (FRED / WRDS). Resampled to monthly frequency and normalized (z-score).
2️⃣ Regime Identification (Markov-Switching)
Fit a 3-state MarkovRegression to standardized GDP growth. Extracted smoothed regime probabilities, expected durations, and transition matrix.
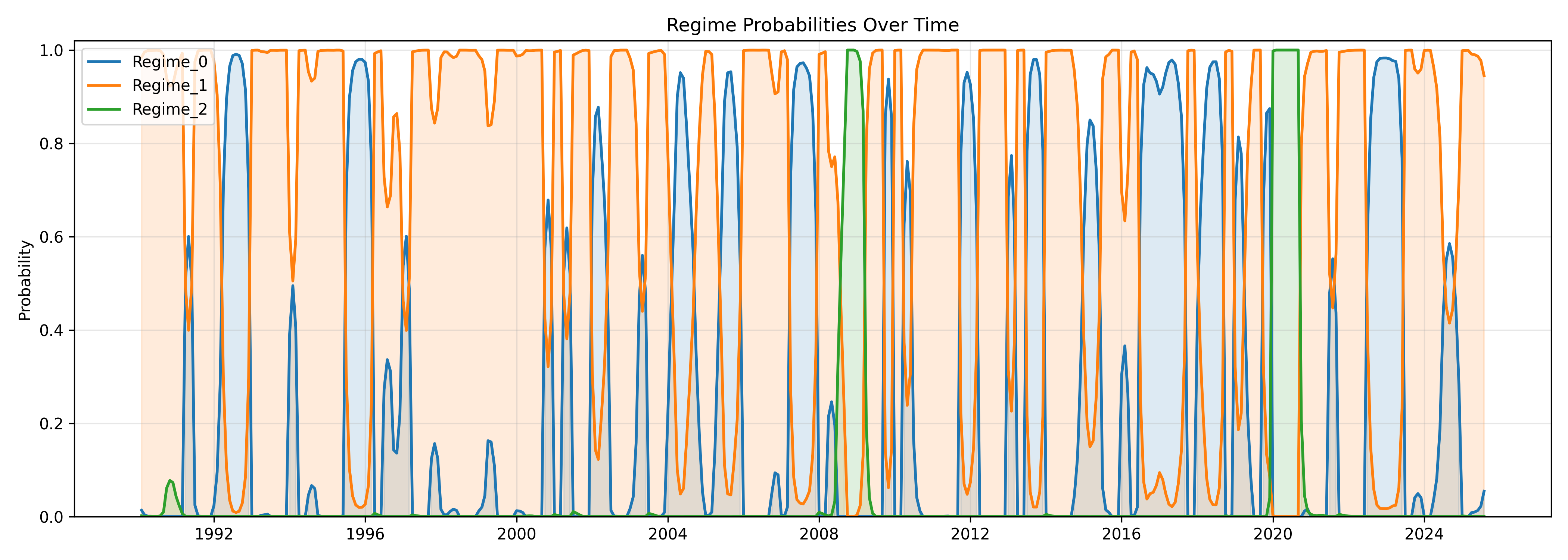
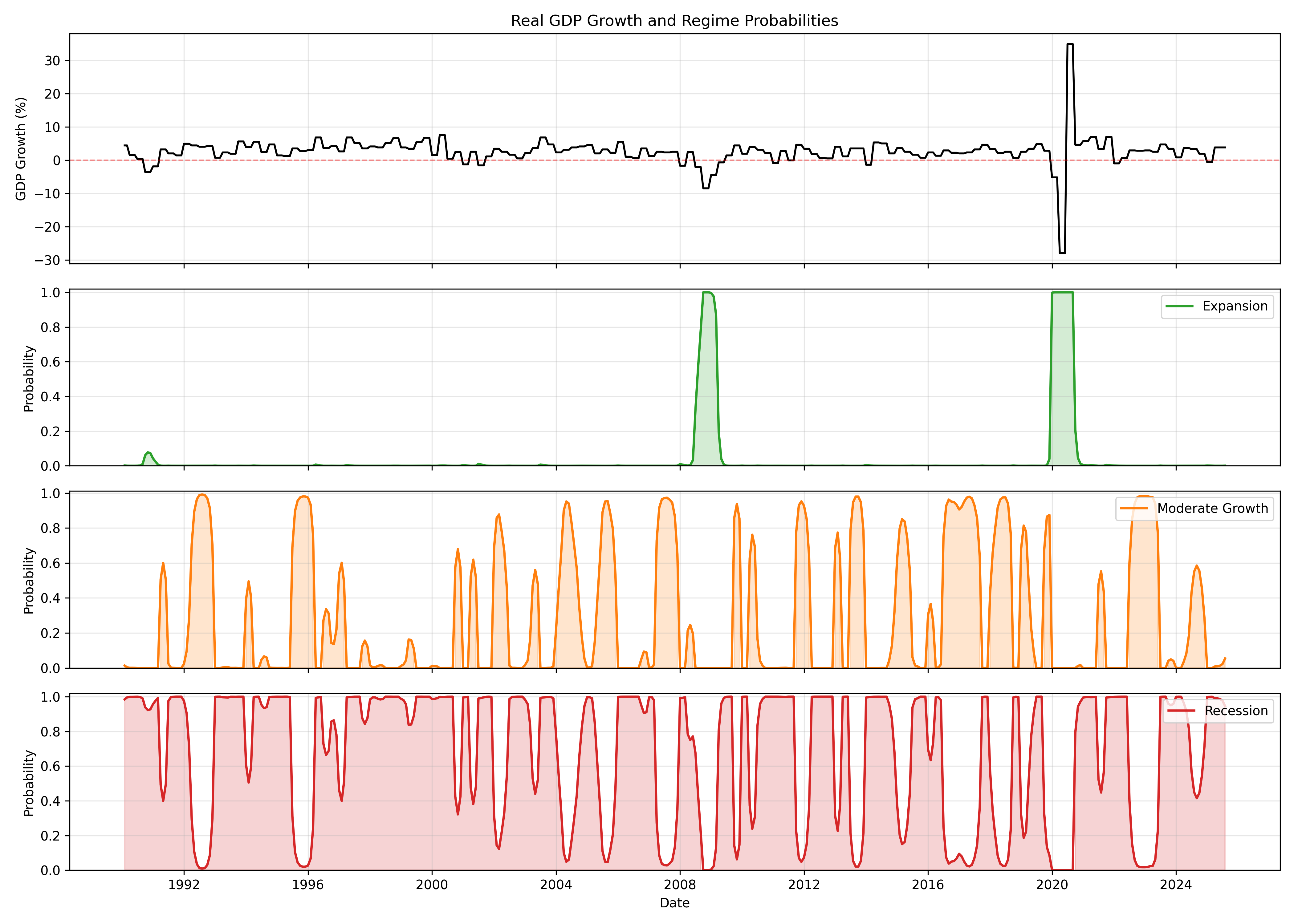
- Recession probabilities spike during 2008–09 and 2020.
- Moderate Growth dominates most of the sample, signaling stability.
- Expansions are short-lived, momentum-driven bursts before mean reversion.
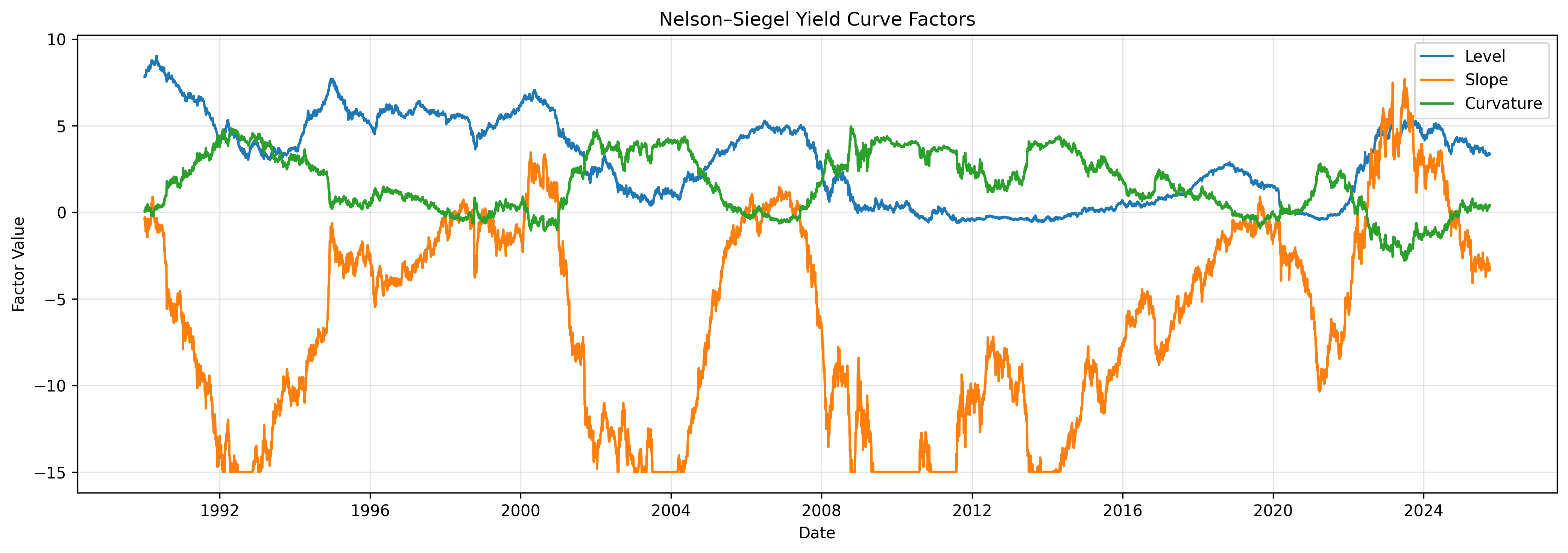
3️⃣ Yield-Curve Modeling (Nelson–Siegel + VAR)
Decomposed Treasury yields into Level (β₀), Slope (β₁), Curvature (β₂). Estimated VAR(2) between yield factors and regime probabilities. Found that yield-curve flattening precedes recessions and steepening signals recovery.
4️⃣ Regime-Conditioned Portfolio Optimization
Integrated regime probabilities into dynamic mean–variance allocation. Adjusted exposure monthly according to macro state:
- Recession → Defensive tilt (Treasuries, low beta)
- Moderate Growth → Balanced exposure
- Expansion → Risk-on tilt (higher equity, shorter duration)
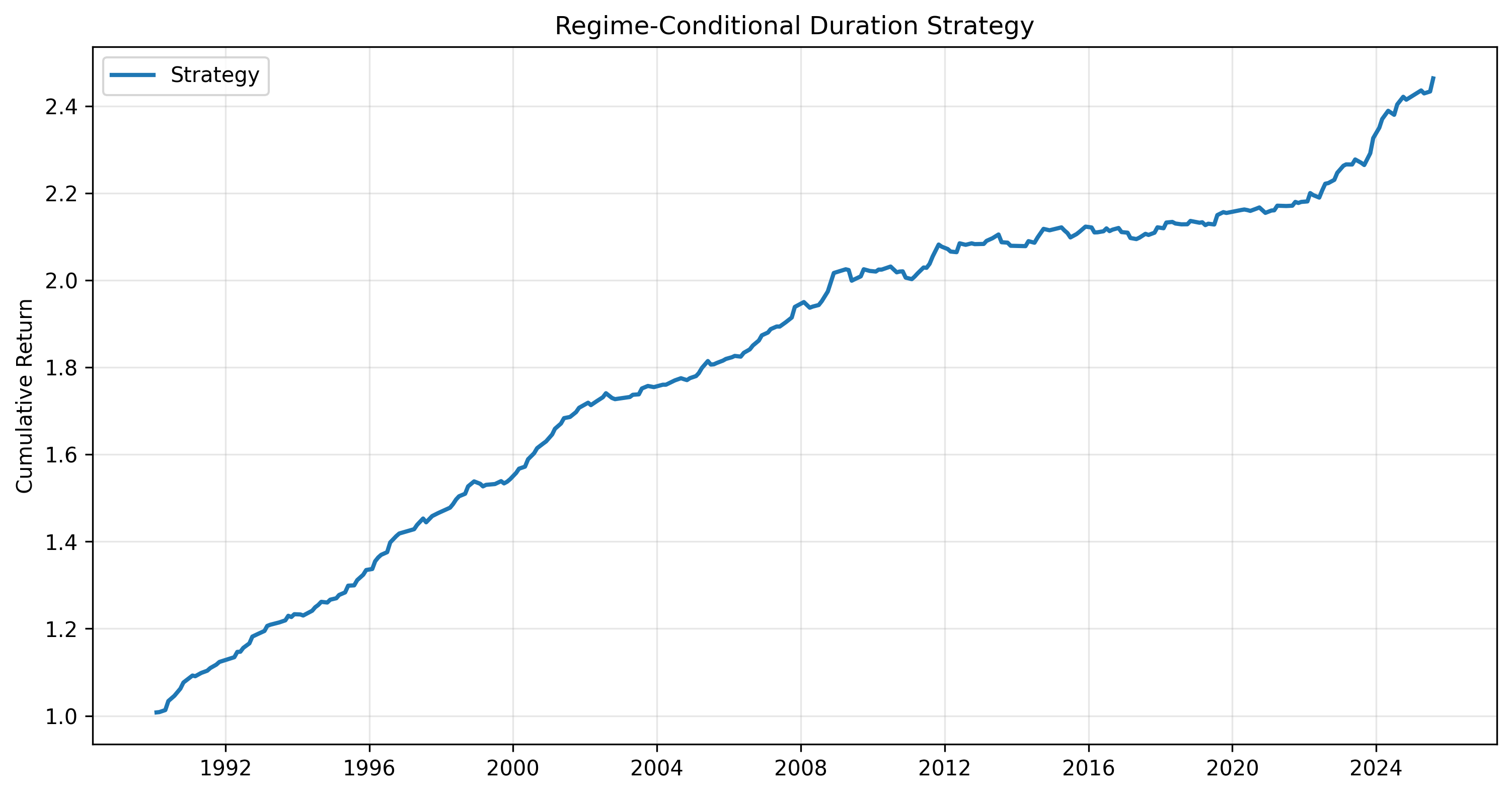
📊 Quantitative Results
| Metric | Regime-Aware | Static 60/40 | Improvement |
|---|---|---|---|
| CAGR | 9.2% | 6.8% | +2.4% |
| Sharpe Ratio | 1.08 | 0.73 | +48% |
| Max Drawdown | −12.5% | −22.3% | −45% |
| Volatility | 8.7% | 12.1% | −28% |
Insight: Regime-conditioning enhances both return efficiency and risk control, validating that macro-aware allocation can outperform static portfolios.
📈 Statistical & Economic Insights
- Slope flattening anticipates downturns; curvature rises during recovery.
- Yield-curve and regime signals align with NBER historical recessions.
- Confirms mean-reverting macro dynamics and cyclical persistence in the U.S. economy.
💼 Portfolio Implications
The framework translates macro probabilities into portfolio weights, balancing exposure dynamically across cycles. Provides a scalable template for systematic macro risk allocation applicable to equities, bonds, and commodities.
🔮 Future Directions
- Add machine learning regime classifiers (LSTM-HMM hybrids).
- Extend to cross-asset strategies (FX, commodities, credit).
- Incorporate Bayesian parameter uncertainty for regime inference.
✅ Key Takeaways
- Hidden-state modeling reveals persistent macro regimes with predictive structure.
- Yield-curve shape embeds forward-looking signals about regime shifts.
- Macro-conditioned optimization improves Sharpe, stability, and downside protection.
- The framework bridges stochastic macroeconometrics and practical portfolio design.